
Zadanie Gra (gam)
Pomóż nam usprawnić bazę zadań!
Game
Limit pamięci: 8 MB
Dwaj gracze, 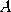 i
i 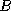 , grają w grę na kwadratowej planszy o rozmiarach
, grają w grę na kwadratowej planszy o rozmiarach  .
Pola planszy dzielą się na białe i czarne. Gra toczy
się jedynie na białych polach.
Każdy gracz ma swojego piona, początkowo ustawionego na
polu startowym danego gracza - jednym z białych pól
planszy. Pola startowe graczy
.
Pola planszy dzielą się na białe i czarne. Gra toczy
się jedynie na białych polach.
Każdy gracz ma swojego piona, początkowo ustawionego na
polu startowym danego gracza - jednym z białych pól
planszy. Pola startowe graczy  i
i  są różne.
są różne.
W każdym ruchu gracz porusza swojego piona na jedno z sąsiadujących z jego pozycją białych pól (w górę, dół, lewo lub prawo). Jeśli gracz przesunie piona na pole zajmowane w tej samej chwili przez piona przeciwnika, otrzymuje dodatkowy ruch (w ten sposób przeskakuje nad pionem przeciwnika). Zauważ, że w takim przypadku kierunek drugiego ruchu może być różny od kierunku pierwszego ruchu.
Gracze poruszają się na zmianę, pierwszy ruch wykonuje gracz 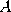 .
Celem gry jest dojście własnym pionem do pola
startowego przeciwnika. Gracz, który dokona tego wcześniej, wygrywa.
W przypadku, gdy ruch gracza składa się z dwóch posunięć i jedynie
przechodzi on przez pole startowe przeciwnika (w sytuacji, gdy
przeciwnik stoi na swoim polu startowym), gracz również wygrywa.
Dla danej sytuacji chcemy stwierdzić, który z graczy ma strategię
wygrywającą (mówi się, że gracz ma strategię wygrywającą, jeśli
może on wygrać grę niezależnie od ruchów przeciwnika).
.
Celem gry jest dojście własnym pionem do pola
startowego przeciwnika. Gracz, który dokona tego wcześniej, wygrywa.
W przypadku, gdy ruch gracza składa się z dwóch posunięć i jedynie
przechodzi on przez pole startowe przeciwnika (w sytuacji, gdy
przeciwnik stoi na swoim polu startowym), gracz również wygrywa.
Dla danej sytuacji chcemy stwierdzić, który z graczy ma strategię
wygrywającą (mówi się, że gracz ma strategię wygrywającą, jeśli
może on wygrać grę niezależnie od ruchów przeciwnika).

Rysunek 1. Jeśli  poruszy się trzykrotnie w prawo
w swoich trzech pierwszych ruchach,
poruszy się trzykrotnie w prawo
w swoich trzech pierwszych ruchach, 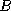 odpowie na każdy ruch posunięciem w górę.
Dlatego, w trzecim ruchu gracz
odpowie na każdy ruch posunięciem w górę.
Dlatego, w trzecim ruchu gracz 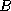 wejdzie na pole zajmowane przez
piona gracza
wejdzie na pole zajmowane przez
piona gracza 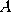 i będzie mógł ruszyć się ponownie. Z tego powodu,
i będzie mógł ruszyć się ponownie. Z tego powodu,
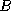 wcześniej osiągnie pole startowe gracza
wcześniej osiągnie pole startowe gracza 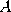 i wygra.
i wygra.

Rysunek 2.  może zacząć od ruchów w prawo i w dół. Później,
zależnie od ruchów gracza
może zacząć od ruchów w prawo i w dół. Później,
zależnie od ruchów gracza 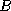 , pójdzie albo w dół, albo w prawo tak,
aby uniknąć spotkania pionów. W ten sposób
, pójdzie albo w dół, albo w prawo tak,
aby uniknąć spotkania pionów. W ten sposób 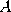 szybciej dotrze do
pola startowego
szybciej dotrze do
pola startowego 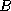 , wygrywając grę. Dlatego też
, wygrywając grę. Dlatego też  ma strategię wygrywającą w tym przypadku.
ma strategię wygrywającą w tym przypadku.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia opis planszy oraz punkty startowe obu zawodników,
- wyznaczy zawodnika, który ma strategią wygrywającą,
- wypisze wynik na standardowe wyjście.
Wejście
Pierwszy wiersz wejścia zawiera jedną liczbę całkowitą  , oznaczającą
liczbę przypadków testowych do rozpatrzenia (
, oznaczającą
liczbę przypadków testowych do rozpatrzenia (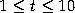 ).
Po nim następuje kolejno
).
Po nim następuje kolejno 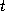 opisów poszczególnych testów.
Każdy z testów jest opisany w następujący sposób. Pierwszy wiersz
zawiera jedną liczbę całkowitą
opisów poszczególnych testów.
Każdy z testów jest opisany w następujący sposób. Pierwszy wiersz
zawiera jedną liczbę całkowitą  (
(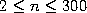 ),
oznaczającą długość boku planszy. Kolejnych
),
oznaczającą długość boku planszy. Kolejnych  wierszy zawiera opis planszy.
Każdy z nich składa się z
wierszy zawiera opis planszy.
Każdy z nich składa się z  znaków (bez odstępów pomiędzy nimi).
Każdy ze znaków to:
'.' (białe pole)
'#' (czarne pole),
'A' (pozycja startowa gracza
znaków (bez odstępów pomiędzy nimi).
Każdy ze znaków to:
'.' (białe pole)
'#' (czarne pole),
'A' (pozycja startowa gracza 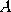 ) lub
'B' (pozycja startowa gracza
) lub
'B' (pozycja startowa gracza 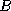 ).
).
Możesz założyć, że istnieje ścieżka składająca się z białych pól,
łącząca punkty startowe graczy 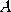 i
i 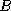 .
.
Dodatkowo, w testach wartych 60% punktów,  ,
zaś w testach wartych 40% punktów,
,
zaś w testach wartych 40% punktów, 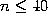 .
.
Wyjście
Dla każdego zestawu testowego na wyjściu powinien znaleźć się dokładnie jeden wiersz zawierający pojedynczy znak 'A' lub 'B', oznaczający gracza, który posiada strategię wygrywającą.
Przykład
Dla danych wejściowych:
2 4 A... .#.. .... ...B 4 A... .... ..#. ...B
poprawną odpowiedzią jest:
B A
Autor zadania: Jimmy Mårdell.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English